
這一堂課,是四年級上學期的分數課,我們從一個八分之一圓聊起。
我給每位學生一個八分之一圓,詢問他們:「這是什麼?」
生:八分之一
我:八分之一個什麼?
生:八分之一個圓
生:八分之一個披薩
生:八分之一個起司
我:剛剛有人說,他是八分之一個圓,代表他是從哪裡分出來的?
生:圓
我:幾個圓?
生:八分之一個圓
我:在他分成八分之一個圓之前,他本來可能是什麼?
生:圓
我:是一個完整的圓嗎
生:是
我:所以,八分之一個圓是從一個圓分出來的,分成幾份?
生:八等份
我:其中的幾份?
生:一份
我:所以,八分之一個圓是從一個圓平分成八份,其中的一份
(複習三年級分數的定義,並且寫在黑板上)
我:你們每人拿到的八分之一圓會一樣大嗎?
生:一樣大
我:為什麼?
生:因為都是八分之一
我:可以證明嗎?
生:把他疊上去
我:好的,你證明一樣了,那麼,我蒐集大家的八分之一圓,有可能可以拼成一個圓嗎?
生:可以,要八個
師:證明給我看

(學生紛紛帶著八分之一圓出來,拼成一個完整的圓)

師:真的也,就跟你們說得一樣。這是一個完整的圓,平分成八份,其中的一份就是八分之一圓,每一個八分之一圓都一樣大。
這是五分鐘的複習活動,喚醒三年級時,對於分數的舊經驗,即使還沒有進入新課程,還是好奇的說,你們剛剛從八分之一圓學到了什麼?
從孩子舊經驗,他們能發現什麼?能不能從「孩子的發現」發展新課程?便是我的挑戰。

生1:我學到一個圓有8個8分之1,每天買披薩就知道披薩有幾了。

生2:我學到8分之1是8份裡面的1份。我學到不管是什麼東西,只要切成8份,裡面的1份就是8分之1

生3:一份披薩分成8份一樣,其中的一份是1/8,二份是2/8,一份是八個1/8組成的。8個等於1個圓。

生4:一份起司有8個,我們從一個圓拿出1/8個。
--------
以上是前10分鐘發生的事情,將決定接下來30分鐘的走向,你覺得哪一個學生的發現,有發展空間呢?
-------
我想從「孩子的發現」發展新課程,從「孩子怎麼學習」的角度去看概念要如何發展出來。
學生3提到:一份披薩分成8份一樣,其中的一份是1/8,二份是2/8,一份是八個1/8組成的。8個等於1個圓。
我順著學生3的說法,繼續追問下去。
師:那麼,其中的三份呢?
生:3/8
師:其中的四份呢?
生:4/8
師:其中的五份?
生:5/8
師:其中的六份?
生:6/8
師:其中的七份?
生:7/8
師:其中的八份?
生:8/8
師:其中的九份?
生:9/8
師:等一下,一個披薩分成8份一樣,其中的9份是9/8,這有沒有怪怪的?
生:要再一個披薩。
師:如果只有一個披薩,平分成8份,可以拿其中的9份嗎?
生:不行
師:這樣看來,要拿八分之九是不可能的,那可以拿八分之十嗎?
生:不行
師:八分之十一?
生:不行
師:從一個披薩平分成8份來看,要拿八分之九個、八分之十個、八分之十一個都不可能,這些分數,被數學家稱作「假分數」,他們都是一個披薩中拿不到的;至於,八分之七、八分之六、八分之五都可以拿到,數學家稱為「真分數」。
(刻意從部分-整體的定義,讓他們自然的接受假分數的名稱,下一堂課再從單位分數累加的定義,自然接受假分數的存在)
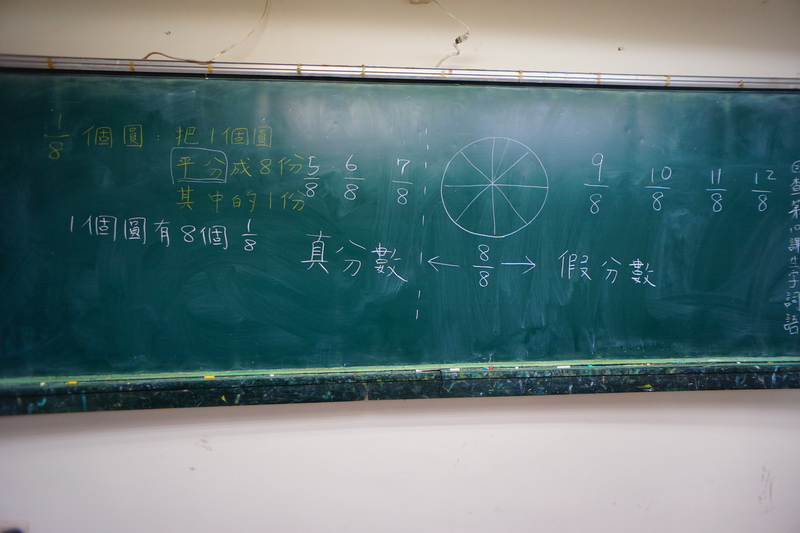
師:不過,聊到這裡,我有個疑問,八分之八呢?你們如果是數學家,你會怎麼歸類?請把你的想法寫在小白板
--------
這裡很冒險,因為依照這個邏輯,要自己想到分到假分數,似乎不太容易。但是,還是希望每到一個思考的轉折點時,先留點時間,讓孩子可以消化、思考一下,先有想法,再來討論。
--------
有些學生會將它歸類到真分數,理由在意料之內:「因為可以平分得到」。

但,出乎我意料之外的是,更多人將它歸類為第三類!

「因為他兩個都是」
(也可以算真分數,也可以算假分數)
「因為他是一份」
「因為已經分完了」
(8/8=1)
「8/8是中間,因為7/8是真分數,9/8是假分數,這樣的話,8/8就沒分配到」
--------
假分數都可以有另外一種形式存在,可能是整數、也可能是帶分數,以這樣的想法來說,8/8歸類成假分數是合情合理。但是,這時候無法以這樣的邏輯去說,因為另外一種形式,是後面才要學到的。
但是,也不想直接宣告,8/8屬於假分數,也不想宣告假分數的定義就是那樣,所以8/8是假分數,如何,比較自然被接受?
--------
師:大部分的人都覺得,8/8應該要屬於第三類,這樣的想法很好,發現了他不一樣的地方。歸類到真分數的,也很有道理。我們看看數學家怎麼想的,今天,我要請你吃起司,如果請你吃八分之一個起司,的確需要把起司平分成八份,給你其中一份;如果請你吃八分之二個起司,的確需要把起司平分成八份,給你其中兩份。
但是,如果要請你吃八分之八個起司,我需不需要平分成八份,然後給你其中八份?
生:不用
師:為什麼
生:因為等於1
師:不用分,整個起司給你就好了,對不對
生:對
師:所以8/8在數學家來看,也是不需要的分數,如果一定要分到真分數或假分數裡面,會分到哪裡?
生:假分數
------------
數學家是不是真的這麼想,不重要。但是,我們就像數學家一樣去想,才是重要的。
-------------

接著,每位學生寫出五個真分數、五個假分數,每人寫出來的都不一樣,但是,從這樣的分類原則,沒有人寫錯。
兩兩彼此核對後,然後到黑板上寫下。頓時,黑板上佈滿了許多的真分數以及許多的假分數,請學生觀察,你們發現了什麼?
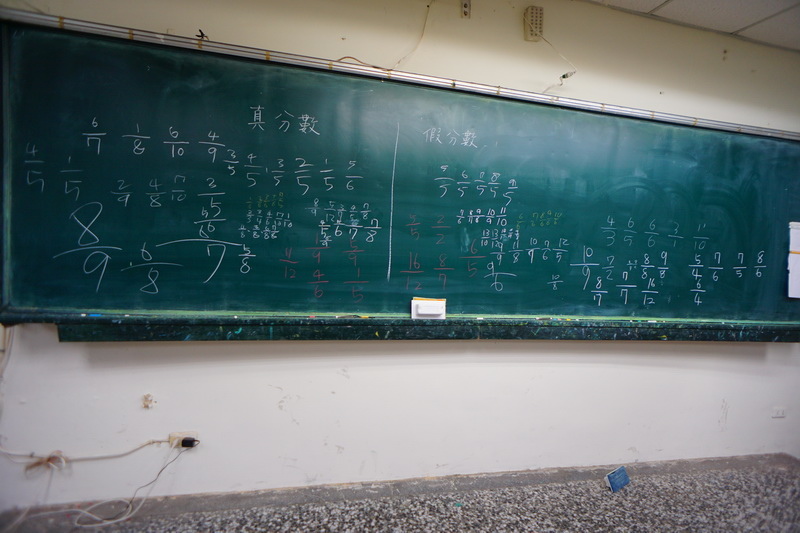
生:假分數的上面都比較大
師:假分數的上面都比誰大
生:下面
師:在分數裡,我們稱上面為什麼?
生:分子
師:下面是什麼?
生:分母
師:所以,你的意思是,假分數誰比誰大?
生:分子比分母大
師:所以假分數的分子大於分母
生:還有
師:還有什麼?
生:還有一樣
師:什麼一樣?
生:分子和分母一樣大
師:或是分子等於分母
師:那真分數呢?
生:分母大於分子
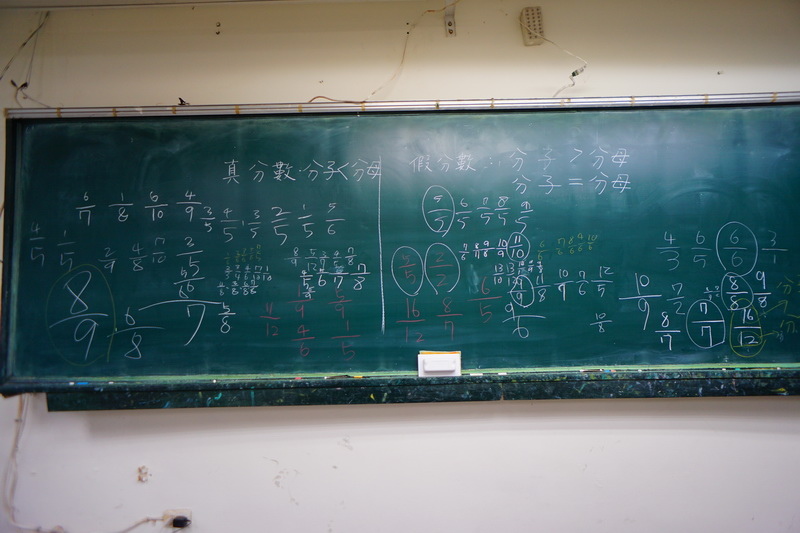
我們從「八分之一圓」,複習分數的部分-整體概念,然後出現不可能的分數、不需要的分數,將它們命名為「假分數」,以及相對的「真分數」。然後,再去找出他們的定義。
假分數:分子大於分母或分子等於分母
真分數:分子小於分母
我在嘗試一種,不是先定義再來把分數分類的路徑,希望他們對於真分數與假分數的名詞會更有感覺。
八分之九是假分數,從一個披薩平分成八份,是拿不到九份的。但是,八分之九真的是不存在的分數嗎?有人昨天其實有提到「需要第二個披薩」,其實,從另一個想法,我們可以找出八分之九的。
我們把八分之一圓,一個一個拿出來看看。
師:兩個八分之一圓是多少?
生:八分之二
師:三個八分之一圓是多少?
生:八分之三
師:九個八分之一圓是多少?
生:八分之九
師:20個八分之一圓是多少?
生:八分之二十
(複習分數是單位分數的累加,這個意義顯然比部分-整體更重要,因為他能發展到加減乘除甚至於擴約分)
昨天,每個人只有拿到一個八分之一,今天我帶來了一箱。等一下,每個人都可以來一把抓,用兩隻手,能抓多少個八分之一就抓多少個!但是,只能用雙手喔!不能碰到肚子,也不能讓它掉到地上,那些掉到地上的,將會被我撿回來。

個個躍躍欲試,準備上來大展身手,卯足勁的抓最多的八分之一圓。

當大家都盡力抓最多的八分之一圓後,下一個任務,就讓抓最多的小孩傻眼。
「接下來,請你們數數看,你抓了多少個八分之一圓?寫在小白板上」

每個人「數數」的方式不同,有人散亂在桌上,一片一片數。

有人則是開始五個五個一疊。

有人則是把他拼成圓,一圈又一圈地往上疊。從孩子自己發想的數數方式,又看到,可以繼續發展下去的空間了。我們就是從孩子的發現,繼續追下去,發現更多的發現。
每個學生抓到的數量不同,因此全班就有好幾個假分數產生。
剛才在數的時候,有些人還會用一些技巧,數起來更快。像是有三個同學是五個五個一疊,有三個同學則是排成完整的圓來算。這讓我好奇,這些假分數,都可以排成完整的圓嗎?
試試看,把你手上的八分之一圓都排成圓,看看最多能排出幾個完整的圓,然後剩下幾個圓。

到目前為止,「帶分數」這名詞還沒有出現,為什麼?因為目前都沒有需求性,就讓他先等著。但是,假分數換帶分數的動作,可以先上場了,從學生數數的過程中,這個動作自然發生了,希望透過湊圓的動作,能讓他們發展出「假分數換帶分數方法」。

原本,想用這個表格,讓學生觀察,發現假分數換帶分數的策略。但是,數數的結果,錯誤有點多,數字也有點大,後來沒從這裡發展,而是簡化數字來發展。

在黑板上貼上12個八分之一,這12個八分之一,是以同樣的方向、同樣的角度,像排隊一樣整整齊齊貼在黑板上,看不出完整圓的樣子。
師:黑板上,有12個八分之一,合起來是多少?
生:八分之十二
師:現在,你們手上都沒有八分之一,你只能看著黑板上的八分之十二,你可以告訴我
可以排成幾個完整的圓,剩下多少個圓嗎?請寫在小白板上
這樣排圓的動作,要如何轉化到紙筆運算?總不能看到假帶互換,就要拿東西來排吧?因此,這一堂課,教具仍然有,但是只有貼在黑板上,學生手上沒有。但是鼓勵學生,如果有需要,可以自己畫。

有學生在操作的經驗以及觀察的過程後,寫出了除法算式。
生:「我把12除以8等於1餘4,所以是1個圓,還剩下4片」。
師:「4片指的是4個什麼?」
生:「八分之一」
師:「4個八分之一是多少?」
生:「八分之四」
因為學生是用直式記錄,我將她的想法用橫式記錄下來,12÷8=1...4,詢問全班,這裡的1指的是什麼?(1個圓)這裡的4指的是什麼?(4個八分之一圓)
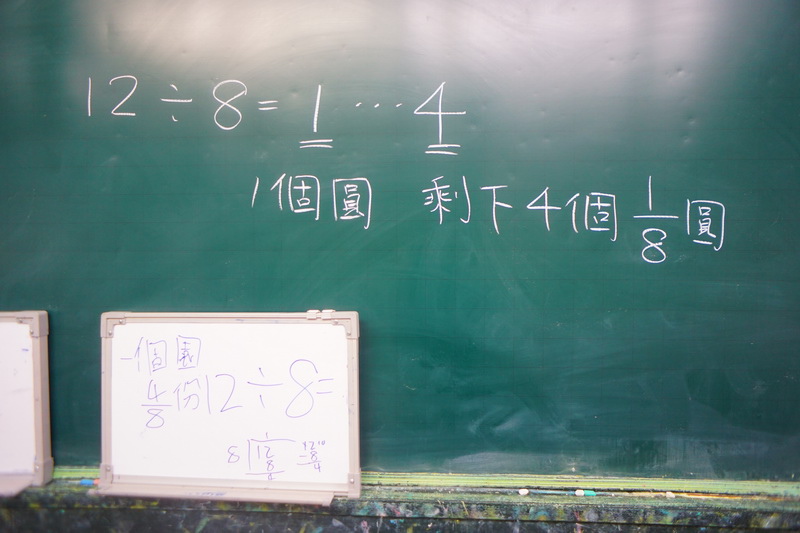
生:老師,我的跟她不一樣
師:你的怎麼不一樣?
生:我是用減的
師:用減的,也可以算出來嗎?
生:可以
師:我喜歡有不同的想法,請你上來分享

這位學生的小白板上,畫了一個大大的圓,平分成八份,每一份都點上一個點點,是點數過的痕跡。在圓的下方,寫了一個算式,12-8=4/8。原來,他把12個八分之一減掉8個八分之一,剩下4個八分之一,寫下了12-8=4,然後又想到這裡的4,指的是4個八分之一,所以在4下方補了分數線以及分母8,變成了4/8。最後,他寫出答案,一個圓又有4/8片。
-------
許多小細節,是可以再精確一點;許多小錯字,是可以再修正一點。但是,現在聚焦在學生的想法能夠大膽說出來,有自信的分享,所以,暫時忽略糾正。
-----------
我把這位小朋友的想法,整理成算式,12-8=4,詢問全班,這裡的4代表什麼?
生:剩下4/8個圓
師:那1呢?這個算式裡沒有看到1,為什麼你可以從這個算式知道,可以排出1個完整的圓?
生:因為減8
師:因為減8,你就知道可以排出1個完整的圓了?
生:對
師:那,如果今天多一點,可以再減八的話呢?
生:2個圓
師:可以再減八
生:3個圓
師:所以,你從「可以減幾個八」就知道可以排出幾個圓了?
生:對
師:太厲害了,真是很棒的想法

一個八分之十二,拿掉教具後,學生居然可以使用兩種策略去解決問題。雖然手上沒有教具,但,腦中其實是用教具在解題的。這時候,我才把12個八分之一排排看,是不是真的像學生說的,能夠排出一個完整的圓,剩下4個1/8。結果,當然跟大家說得一樣,1個圓還有4/8個圓,為了表示這樣的圖案,我們把1和4/8合在一起,寫成一又八分之四,代表有1個完整的圓,還有4/8個湊不滿完整的圓,而12/8經過湊圓後,排出一又八分之四,不會變多、也不會變少,所以可以畫上等號,他們是一樣大的。
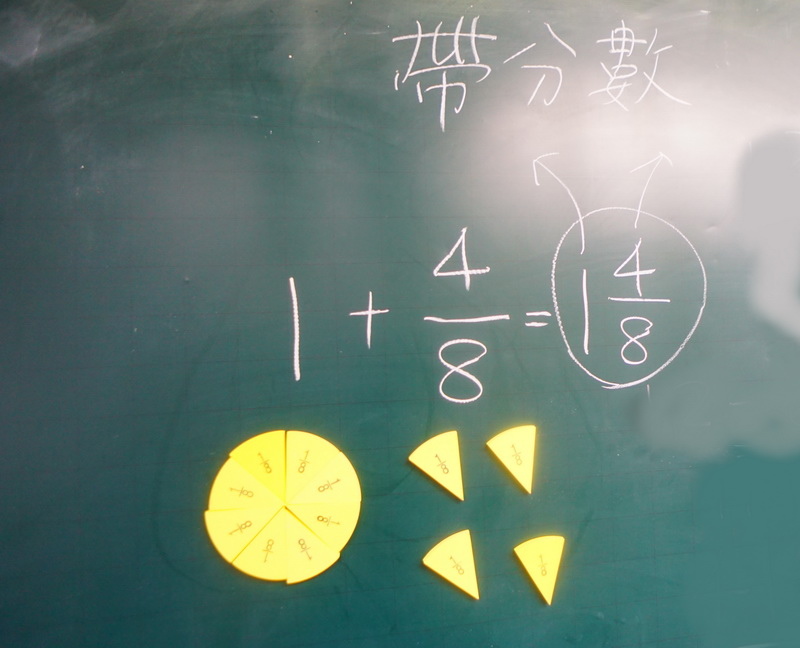
帶分數的名詞,我們在這裡才出現。因為,這時候,是它該登場的時候了。也告訴孩子,剛才在做的事情,就是把假分數換成帶分數的過程。
師:剛才你們把12/8這樣的假分數,換成了1又4/8的帶分數,我很好奇,你們也能做其他的題目嗎?要不要挑戰一題?
生:好
(就是要這樣有自信的聲音)
師:試試看,把八分之四十一換成帶分數
假分數換帶分數,要背分子除以分母,商等於整數,餘數等於分子嗎?背出這樣的孩子能說出「分子除以分母」是什麼意思嗎?
透過八分之一排圓的過程,崇德四年級的孩子,已經有了兩個解決策略,第一個是減法策略,第二個是除法策略,這時候,居然又出現第三個策略!
他不是用減法,也不是用除法的,而是乘法跟加法!
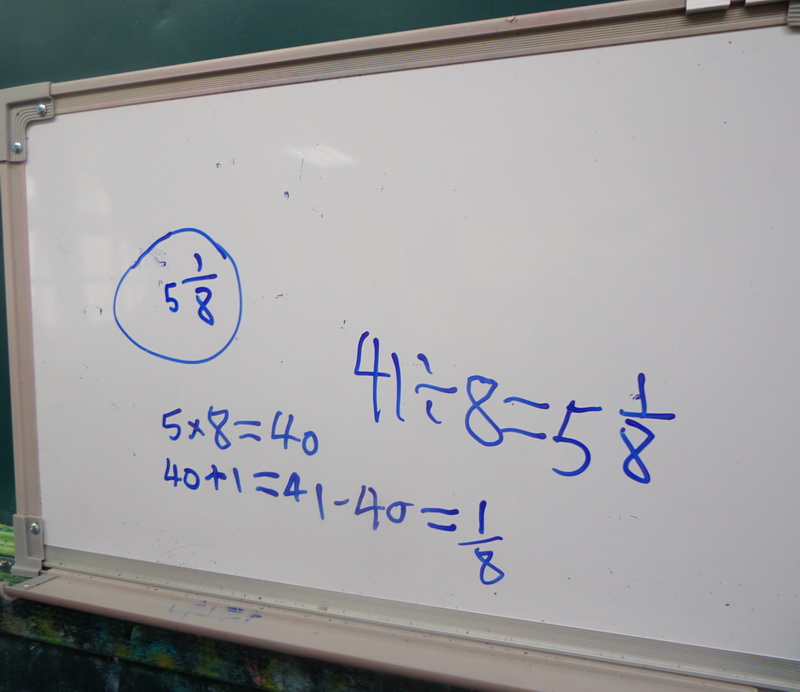
5×8=40,40+1=41,41÷8=5又1/8
先乘後加,直到41個八分之一算完為止。
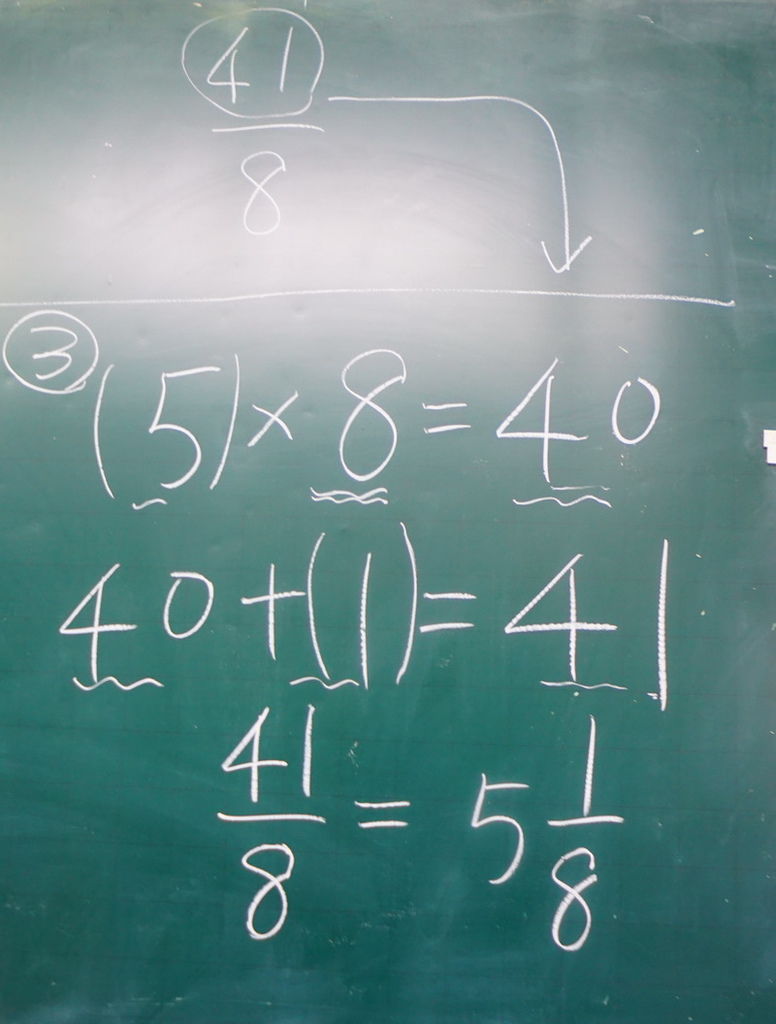
這是假分數換帶分數的第三個策略,全班才10個人,居然發展了三種解決假分數換帶分數的策略,跟都市學校相較,毫不遜色。
那反過來呢?帶分數換假分數,也可以拿出自己的策略嗎?請把六又四分之三換成假分數。
-----------
我們離八分之一圓越來越遠,改成以四分之一為單位,而且不是假換帶,而是帶換假。這時候,就會看到有人還是想要用除的,可是到底是六除以四,還是三除以四,還是.....?總是有人看到題目,就拿起數字不思考的列式。這倒也不用急,面對新的挑戰,想要用剛剛學會的東西來解決問題,是合理的現象,至少,表示剛剛的除法列式,他有認真在聽。
------------
再給一點鷹架。我在黑板上寫下,六又四分之三等於六個圓加四分之三個圓,等於四分之括號。用圓來喚醒他們操作的記憶。
------------
慢慢的,有人開始回到畫圖去想了,甚至於越寫越完整,就像十一號女生。

她寫著,6個圓=24個1/4;24個1/4+3個1/4=27個1/4;答:27/4。
美中不足的是,她把第一個式子直接連加到第二個式子,寫成6個圓=24個1/4+3個1/4=27個1/4。
但是,你可以確定,她的觀念非常非常的清楚,而且,她已經很熟悉,把單位分數拿來作為計數工具了,接下來的分數加減法和分數乘法,相信都不會是問題了。
------------
但是,班上不是只有頭腦靈活的,也有對自己沒有信心,常常布題後,就一片空白、不知所措的。在前幾次布題挑戰時,都需要老師過去個別指導一下。但指導完,即使寫對
也馬上擦掉,還怕被別人看見。
這一題,我依然個人指導,開始跟他一問一答。
師:六又四分之三有幾個完整的圓?
生:六個
師:那你先畫出六個圓。
生在小白板畫了六個圈圈
師:一個圓可以分成幾個四分之一?
生:四個
師:你可以在圖上表示出來嗎?
生在每個圓圈上,都寫上一個4
師:六又四分之三,除了這六個圓,還有什麼?
生:四分之三
師:四分之三有幾個四分之一?
生:三個
師:那你畫一個小圈圈,代表剩下的圓
生畫了一個小圈圈,裡面寫上3
師:現在,這裡會有多少個四分之一?怎麼算?
生:全部加起來?
師:很好,就這麼做
生在小白板寫下4、4、4、4、4、4,以直式排列著,用直式計算算出24,然後再寫一個直式24+3=27。
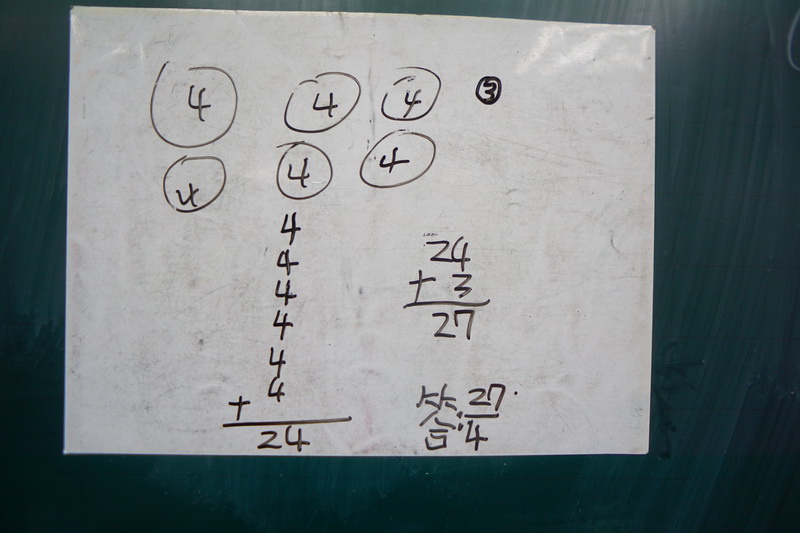
師:27代表什麼?
生:27個四分之一
師:27個四分之一就是...?
生:四分之二十七
師:你寫個答
生寫「答:27/4」
師:你可以把這一題的想法,重頭說一次給我聽嗎?
生:六又四分之三有六個圓,每個圓有四個四分之一,所以全部加起來就是24,然後還有3個四分之一,加起來就有27個四分之一,答是四分之二十七
師:你說得很棒,可以說給全班聽嗎?
生點頭
當他站在臺上,把剛剛那一段話,講給全班聽時。我卻想到之前一看題目就直接說我不會的他;我卻想到人家在解題時卻在罵隔壁你不會的他;我卻想到當大家都已經寫完卻仍一片空白的他。無論這是曇花一現,或是明天仍回到原狀,這一分鐘,卻是我最珍惜的一分鐘。因為,終於等到你上臺了....
八分之一圓是從以下網址訂購的



 留言列表
留言列表
