快樂是自找的

質數的定義太抽象，對於小學生來說，真的是定義的莫名其妙，難以理解數學家定義質數之美；初學者在六年級一開始，就要開始找質數，也沒有學習需求，如何啟動孩子的學習開關？

我們這次嘗試將數學奠基模組中的長方形數，進入五年級因數的課堂中，希望透過遊戲與操作，讓因數、質數都能成為圖像化，真正達到有圖有真相的境界。

道具是圍棋子。首先，先拿一顆棋子告訴學生，這是一個點點，只是放大了，讓我們比較容易看。

現在有兩個點點，兩個點點可以連成什麼？一條線。

三個點點，我把他們這樣擺，也可以連成什麼？一條線。如果把第三個點點換個位置，就可以連成三角形，不過，今天的遊戲是要排長方形或正方形，所以，其他圖形我們先不管他。

四個點點，我們這樣擺，可以連成什麼？還是一條線。

換個位置，我們讓點點跟點點之間的距離一樣，這時候就可以排成什麼？正方形。因此我們說，4是一個正方形數，他可以排出一個正方形。

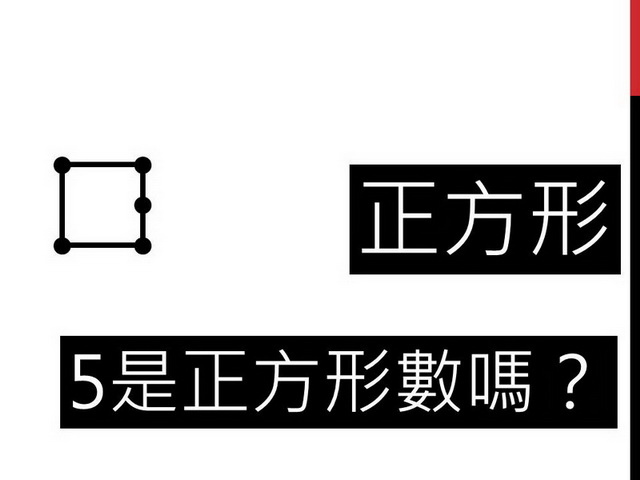
5是正方形數嗎？五個點點可以排成正方形嗎？或許有學生覺得可以，把點點放到線上，一樣圍成一個正方形。當然，我們肯定學生的想法，不過，這也將會是遊戲的漏洞，這會導致4以上的數字都能排成正方形，就沒有挑戰性了，所以，我們加了一條遊戲規則。

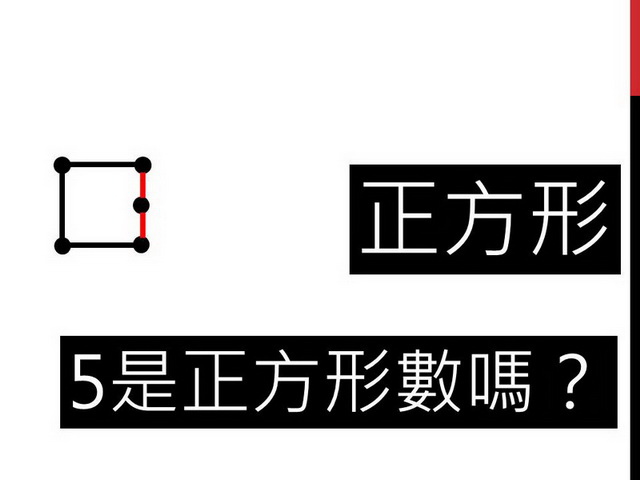
點點跟前後左右的點點距離都要一樣才可以。第五個點點跟前面和後面的距離是「紅線長」，但是其他點點之間的距離都是「黑線長」，「紅線長」和「黑線長」距離相同嗎？不相同，所以，這樣的排法，在遊戲中是不被接受的。將第五個點點放到別的地方，都無法圍出正方形，所以，5不是正方形數。

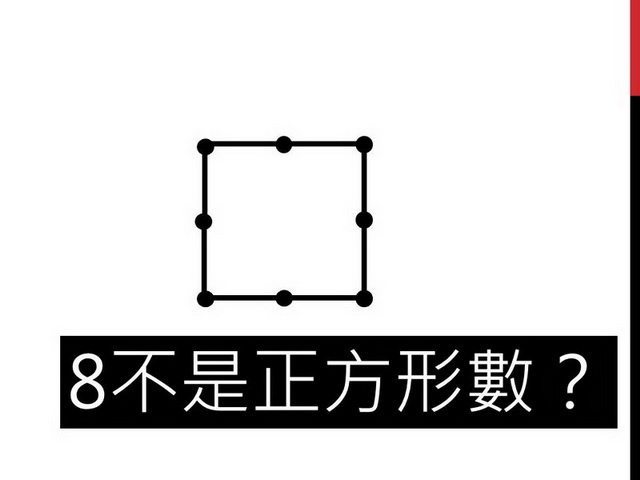
8是不是正方形數？或許學生會圍出這樣的圖形，認為8是一個正方形數。

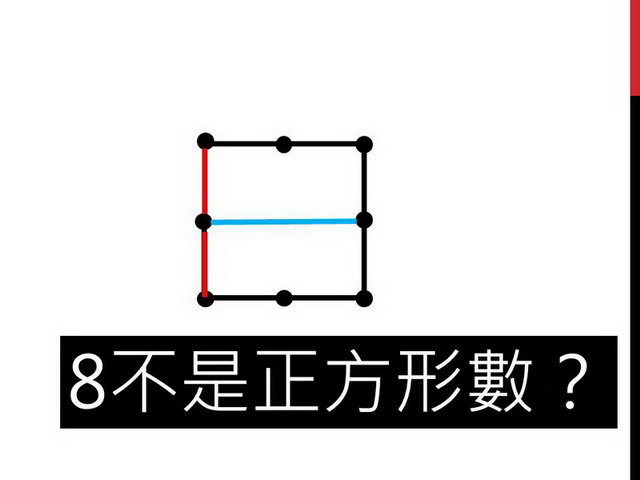
但是，我們可以發現第二排的點點，和前後點點的距離跟左右點點的距離是不相同的，根據剛才增加的遊戲規則，這樣是不會允許的，因此，我們可以發現，空心的正方形都是不允許的，因為那一定會有點點跟點點的距離變得很長。

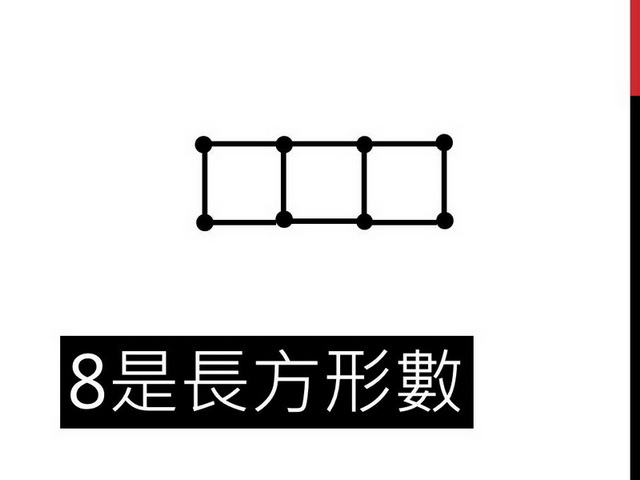
8雖然不是正方形數，但是可以排成長方形，而且點點跟前後左右的點點距離都一樣。在今天的遊戲中，我們就是要挑戰正方形或長方形，只要能排出來，就可以得分。

比賽時兩人一組，一組拿到30顆棋子。猜拳後，由獲勝者先出題，從1到30中選一個數字，讓對手排出正方形或長方形。

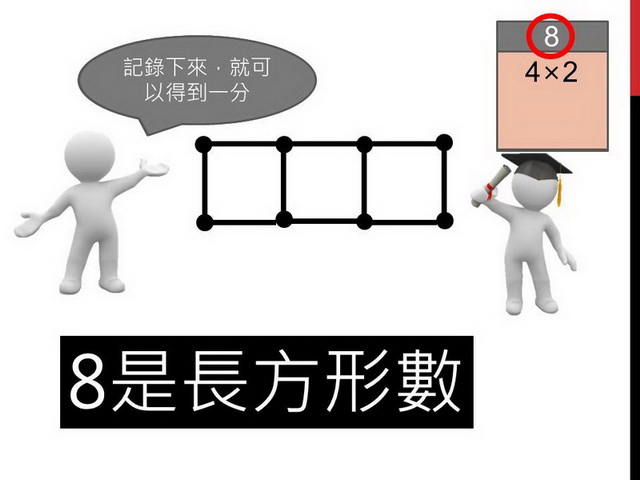
示範者出題8，對方排出來了之後，必須記錄到紀錄紙上。先將8這個數字圈起來，表示目前挑戰的是這個數字，接著將排出來的圖形用算式紀錄下來，每排有4個、總共有2排，因此記錄成4x2，得到一分。

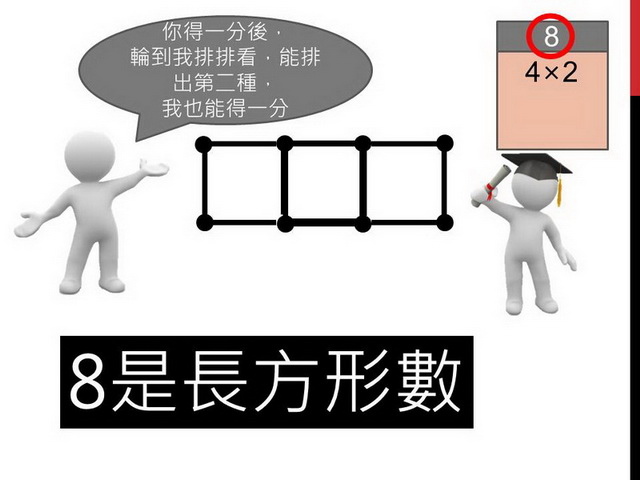
對手排出一種後，就要把棋子交給出題者，由出題者排排看，如果能排出第二種，那麼，出題者也可以得到一分。

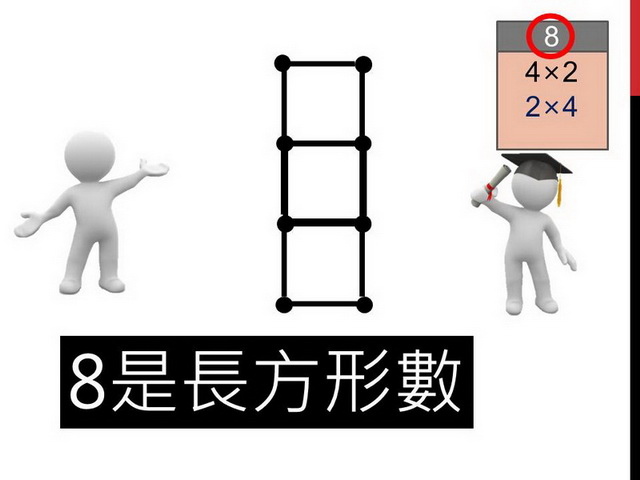
出題者將剛剛的長方形旋轉了90度，變成了一排有2顆、總共有4排，記錄成2x4，出題者也得到一分。

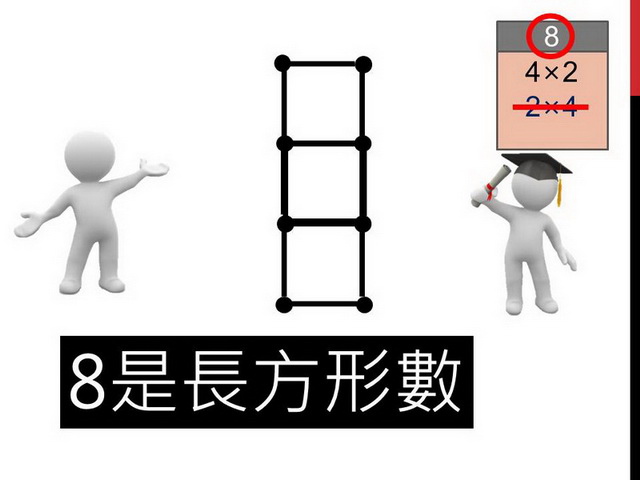
這樣顯然不太公平，出題者只是將對手的棋子旋轉90度，從算式來看，也只是把被乘數與乘數互換，就可以獲得一分！為了讓比賽更公平，新增一條遊戲規則，旋轉90度會相同的，也就是把對方的被乘數與乘數互換而已，這樣是無法得分的，因此在這場比賽中，4x2已經排出來了，2x4就無法得分了。

規則說明完畢，各自開始比賽。

關於「排的技術」，可以視情況全班一起說，或是一組一組提示。

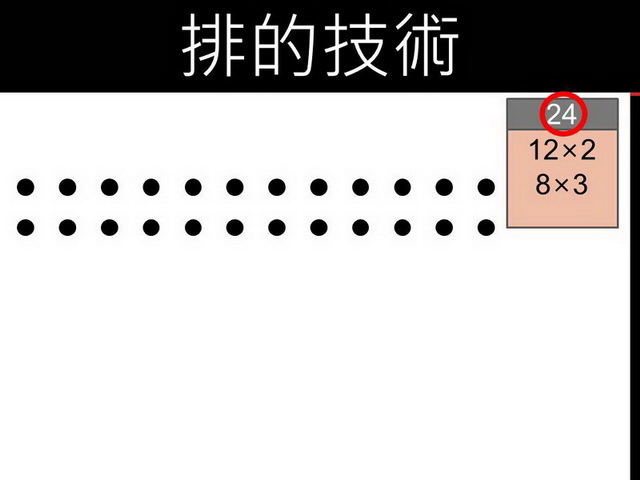
在排24這個數字時，我們可以把棋子兩個兩個一排，排排看，最後會不會剛好排完，如果會，那就可以獲得一分。

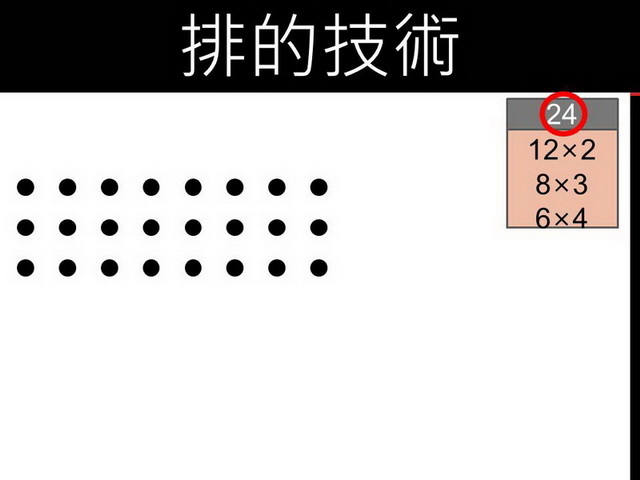
兩個、兩個一排排完之後，棋子不要弄亂，再試試三個、三個一排。

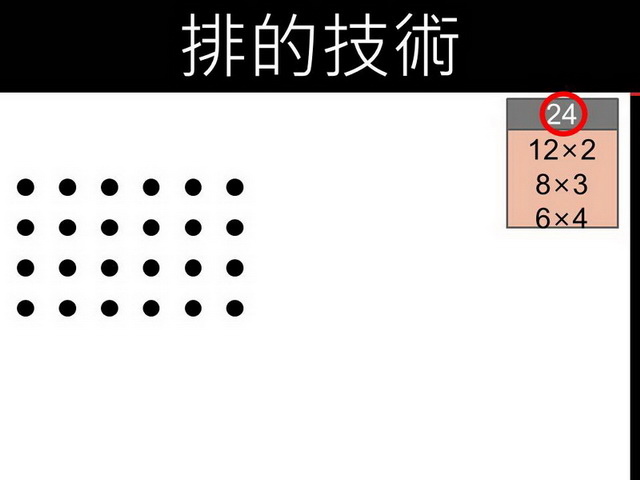
三個、三個一排也剛好排完，那太好了，也可以得分。接著，再試試四個、四個一排，依照順序去試，就不會漏掉。

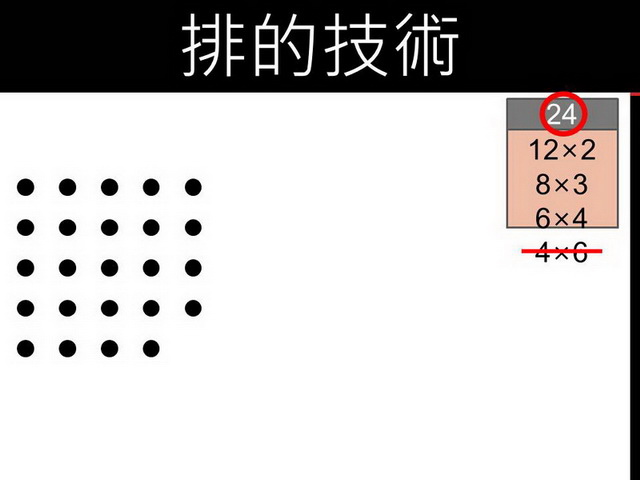
五個、五個一排，結果剩下4顆棋子，代表5不行，別氣餒，再試試下一個數字─6。

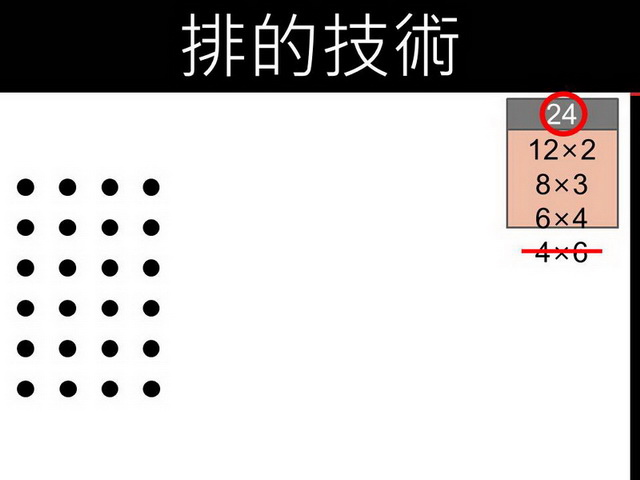
六個、六個一排，結果又剛好排完，太好了！只可惜，6x4和剛才的4x6是交換關係，所以無法得分。這時候，若學生發現，已經不用在往下找了，那就太棒了，這可以類化到找因數時，看見黃金交叉時，就可以停止了。

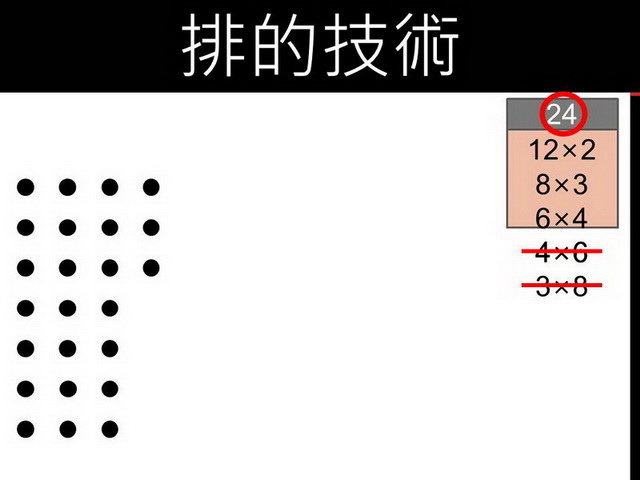
當然，若學生仍然看不出來，就繼續七個、七個一排，接著八個、八個一排，又回到8x3，還需要再九個、九個一排嗎？

玩著玩著，會有人發現，其實不需要排，可以用算的，那麼，就能請他分享如何用算的。

通常學生會回答用九九乘法表，但是，有些是不在九九乘法表內的，比如2乘以多少才會等於30，這時候，就可以利用乘除互逆，將30除以2得到15。後面再加個餘數為0，讓學生發現，這些可以排成長方形或正方形的算式，餘數都是0，此時就帶入數學名詞─整除。

一節課玩不完，有些學生下課會繼續挑戰，慢慢就把1到30的所有可能全部找出來，就算找不完，也沒有關係，先讓遊戲結束，計算彼此得分，可鼓勵得高分的學生，再鼓勵對手得低分的學生，因為，有可能他都找到排不出正方形或長方形的數字！

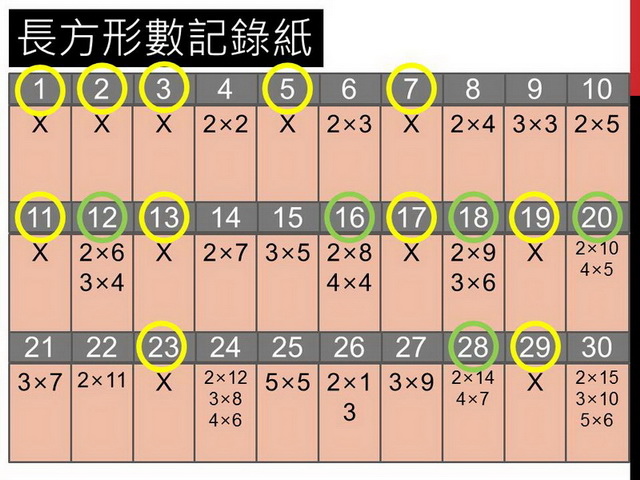
最後，我們來找出獲勝秘訣吧！看看這張計分單中，哪些數字會讓對手得不到分？一一找出打叉的數字，並用黃筆圈起來。有些數字，雖然會讓對手得一分，但是自己也能得到一分，就像是綠色圈起來的數字，總共有兩分價值的數字。我們把這些數字分類，總共有相同分數價值的數字就擺在一類。

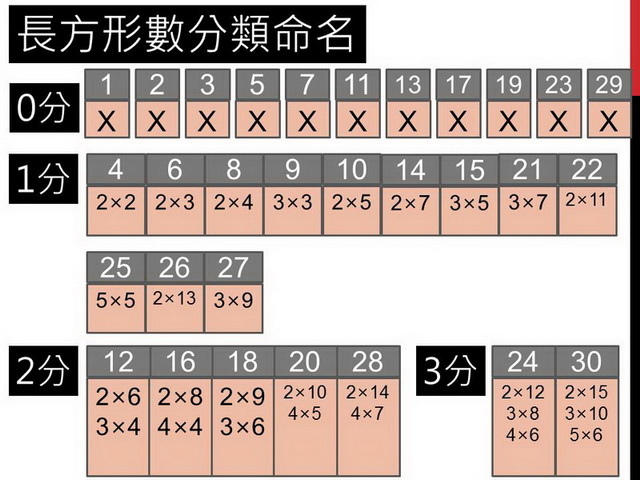
在遊戲中，如果你遇到對方出總分是0分的數時，你的心情是什麼？你的感覺是什麼？為這些數字取個名字。同樣的，總分是1分的、2分的，都試試為它們取名。

一開始，學生只有鴨蛋數、零零數，這種跟「0」這個數字相關的名稱，和遊戲內容與棋子排列本質扯不上關係。後來，再慢慢引導與鼓勵後，有學生提出「討厭數」，詢問為什麼？學生說，「怎麼拚都拼不出來很討厭」。哇！我就開始興奮了起來，總算從遊戲經驗去命名了。

「搞笑數」，因為拚了很久才發現，原來是拚不出來的，很搞笑。

「勝利數」，因為出這個數字就會勝利。

「不算數」，因為（沒有人會得分）不會算分數。

慢慢有了學生的「創作」產生，我喜歡學生在課堂上有思考，有自己的想法，有自己的創作產生。在這堂課的後面慢慢發酵了。

那麼總共得１分的數請取個名字。

「搶分數」，因為只有一種方式可以得分，所以要用搶的。

「單獲數」，只有一個人可以獲得分數。

總共得２分的數請取個名字。

「平分數」，因為一人得一分。

「公平數」，因為每個人都可以得一分，所以很公平。

總共得３分的數請取個名字。

「危險數」，很危險，可能一下就輸給人家很多。

「強奪數」，搶了我好多分。

「快樂數」，我一次可以得很多分。

瞧！創造力的出現，讓人很驚喜。

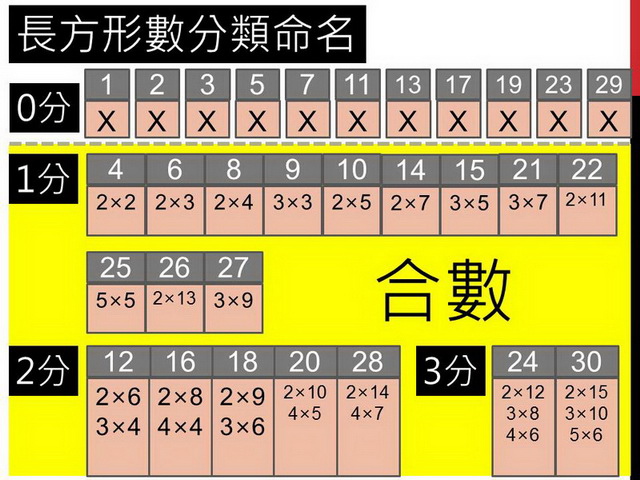
最後，讓小朋友知道數學家的命名。可以排成長方形或正方形的數字，數學家統統稱為「合數」，這些至少都有一分的價值。

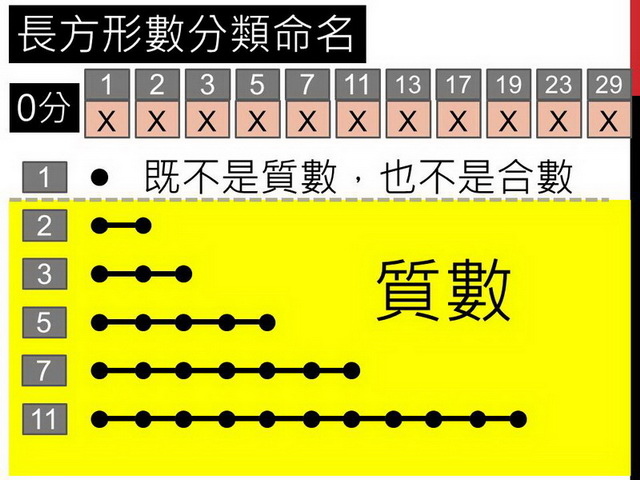
至於只能排成一條線的，沒有得分價值，則稱為「質數」。

至於1，連一條線都排不出來，因此數學家稱他「既不是質數，也不是合數」。

「我覺得我們取的名字比較好，數學家取的名字沒有我們有創意」

哈哈哈哈，是啊，數學課不只是建築知識，同時也是建築孩子的自信心，你可以比數學家還棒！而質數和合數都成為了看得到、操作得出來的數學名詞，而不是抽象的概念了。

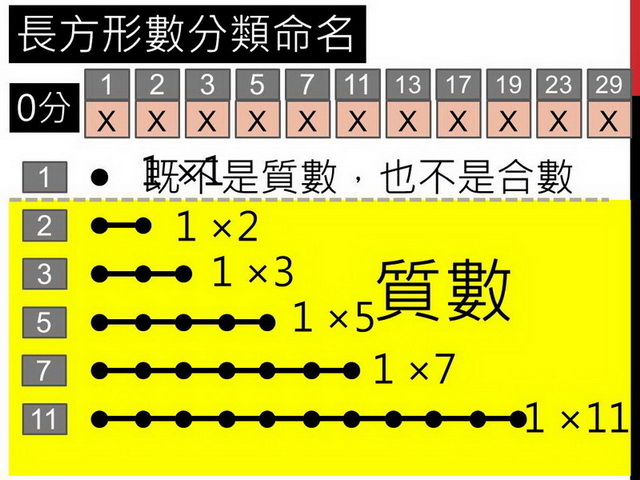
接著，觀察這些質數，雖然不能像那些可以得分的數，寫成2x4或3x5之類的，但是就算只能排出一條線，也能寫出算式吧？2可以寫成1x2，3可以寫成1x3，5可以寫成1x5……。

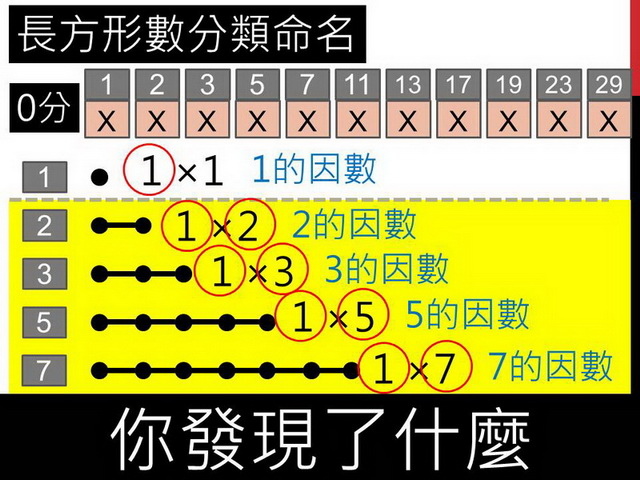
像這樣，一個數可以分解成兩個數字相乘時，這兩個數字，數學家就稱他們是原本數字的「因數」。因此1的因數有1，2的因數有1、2…。觀察質數的因數，你發現了什麼？

個別解題，每個人寫下自己的發現。

雖然全班只有13人，也能寫出很多種發現，經過歸納後，將學生的發現透過討論與發表，進行全班澄清與語句的精準化。

發現一：「有規律性」

有三個學生這樣寫，雖然不是預設的學習目標，但是，第一次嘗試寫下發現，小朋友猶豫很久，還會不斷跟老師確認，想知道這個答案是不是老師要的。

我不是要你寫「我要的答案」，我是要你寫「你的發現」，「你的發現」可以很多，也可以來自任何想法，都沒有標準答案，那是提供大家可以一起學習的想法。如果這個發現是錯誤的，那也會讓大家學到，原來這是個錯誤的發現，有什麼環節是我沒有想到的。學習錯誤的發現，也是件很重要的事情。

「有規律性」是個很好的發現，更進一步的，能不能再發現有什麼樣的規律性？

發現二：都是乘出來的

的確，在描述一條線的時候，我們都用乘法來表示。然後才將這些相乘的數，稱為是它的因數。

這也是個好發現。

發現三：因數是用乘算出來的

老師：「像這樣可以拆解成兩個整數相乘的時候，這兩個整數就是它的因數。」

結果學生寫出的發現：「因數是用乘算出來的。」

雖然是循環關係，不過，對於初步寫想法的學生來說，任何一個想法，都是有價值的想法，可以給予鼓勵。

發現四：都是一條線

老師：像這樣只能排成一條線的數，我們就叫做質數。

學生：我發現質數都是一條線。

等待好的想法，是需要有耐心的，即使是循環關係，仍然鼓勵孩子發表。

發現五：每一個都有1出現。

這已經有碰到邊了，其實再引導一下，就會有很漂亮的發現。

發現六：我發現了因數都有1，不管是什麼因數都會有1。

漂亮！我們慢慢從圖像的定義進入到數學定義了。而這個發現，在合數的時候，還可以讓學生再確認一次。

發現七：只要是1都是自己

這個發現其實不太清楚要表達的是什麼，連學生也說不出來，不過，任何一個想法都是好的，因為有可能幫助大家引導到更完整的想法出現。

發現八：1x1還是1；1x2還是2；1x3還是3；1x5還是5；1x7還是7

這個學生的「還是」是個關鍵，將1的乘法性質，用「還是」呈現，貼切又貼近大家。

發現九：1x1=自己；1x2=自己；1x3=自己；1x5=自己；1x7=自己

這裡把「自己」這個詞放進來，又更進一步了！因此，請他出來分享，追問這算式的意思就是5的因數有什麼？

「5」

「7的因數有…」

「7」

「11的因數有…」

「11」

「285的因數有…」

「285」

「9523的因數有…」

「9523」

於是歸納出來

質數的因數都是1和自己。

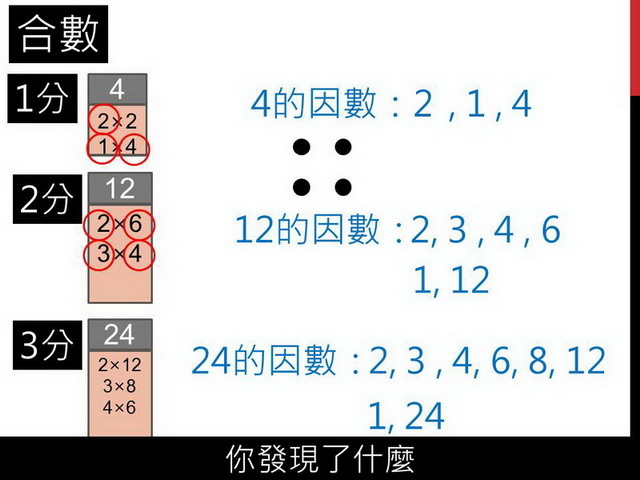
那麼，合數呢？我們觀察合數，除了剛剛可以得分的那些數字外，是不是也都可以排成一條線？排成一條線時，如何用乘法表示？於是，補上了每個合數的兩個因數。

從合數的因數，又可以發現什麼？

發現一：合數乘的很多，質數乘的少，2個。

要寫出完整意思的句子，似乎仍然有點困難，但是可以看到他們的發現與意思。

發現二：合數最少3個，質數的因數都只有2個

雖然句子也不完整，但是合數的因數個數有3個以上，這件事情由學生發現，就是件令人振奮的事情。同時，也發現質數的因數個數都只有2個。

發現三：合數的因數最多有8個。

雖然是錯誤命題，但是也是個很好的論證例子，因為舉例的是1分數、2分數、3分數，最大的是3分數，比如說是24，因數個數除了2x12、3x8、4x6，還有剛剛發現都會有1和24，總共加起來只有8個因數，所以認為因數最多是8個。不過，可以讓學生再去找找看，會不會有超過8個因數的數字，找到一例去反證，也或許可以留到學過倍數後再回來看看。

透過這個奠基模組，我們經歷了因數的具體象徵，窮盡因數的方法，也看見了質數與合數的圖像，然後回到抽象的定義，希望透過這樣的過程，讓學生不只是玩得開心，也能學得豐富。

活動改編自數學奠基模組─長方形數（林福來教授）。

改編者：花蓮縣崇德國小朱志青

教學者：花蓮縣崇德國小嘎啷